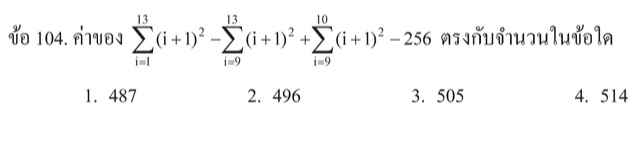แบบฝึกหัดลำดับและอนุกรม

เขียนสูตรให้ดูก่อนค่ะ

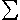
ค่าคงที่ = ค่าคงที่จำนวนข้อมูล

n

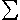i=1

i =

n(n+1)

2

n

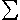i=1

(i²) =

n(n+1)(2n+1)

6

--------------------------------------------

ข้อนี้ ลองสังเกตที่เลขเริ่มต้น(เช่น i = 1) และเลขสุดท้ายของซิกมา (เลขบนเครื่องหมายซิกมา)

13

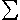i=1

(1 + i)² -

13

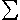i=9

(1 + i)² +

10

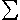i=9

(1 + i)² - 256
พจน์แรก เขียนแยกได้แบบนี้ (ดูสีแดง)
ถ้าดูไม่ออกให้สังเกตเลขเริ่มต้น กับ เลขจบของซิกมา
=

8

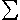i=1

(1 + i)² +

13

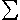i=9

(1 + i)² -

13

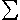i=9

(1 + i)² +

10

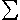i=9

(1 + i)² - 256
จะมีตัวที่ลบกันได้ คือ พจน์ที่ 2 กับ 3 จะเหลือแค่
=

8

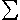i=1

(1 + i)² +

10

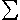i=9

(1 + i)² - 256
พจน์แรก กับพจน์ที่สอง ต่อกันได้พอดี ดูเลขตัวแรกจบ 8 แล้วตัวต่อไปต่อด้วย 9 แล้วไปจบที่ 10
งั้นเขียนรวมได้แบบนี้ค่ะ
=

10

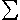i=1

(1 + i)² - 256
กระจาย (1 + i)² ก่อนค่ะ ต้องกระจายแบบกำลังสองสมบูรณ์นะ
=

10

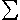i=1

(1 + 2i + i²) - 256
= กระจายซิกมาเข้าไปในวงเล็บได้
=

10

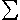i=1

1 +

10

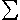i=1

(2i) +

10

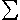i=1

(i²) - 256
=

10

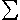i=1

1 + 2

10

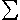i=1

i +

10

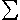i=1

(i²) - 256
แทนสูตร
= (110) + 2(

1011

2

) + (

101121

6

) - 256
= 10 + 110 + 385 - 256
= 249 ตอบ

ไม่มีช้อยที่ถูกค่ะ