ถามโจทย์อนุกรมเรขาคณิตครับ

สมมติให้ อนุกรมเรขาคณิต เป็น
a + ar + ar² + ar³

ตั้งสมการตามที่โจทย์บอกค่ะ
ผลบวก 4 พจน์แรก = 15
a + ar + ar² + ar³ = 15 -------(1)

ผลบวกของกำลังสองของแต่ละพจน์เท่ากับ 85
a² + a²r² + a²r⁴ + a²r⁶ = 85 -------(2)

สังเกตว่า ติด 2 ตัวแปร คือ a, r และมี 2 สมการ แก้ระบบสมการค่ะ
จะได้ค่า a,r แล้ว ก็เอาไปแทนในอนุกรม จะได้แต่ละพจน์
โจทย์ถามผลพจน์ 4 พจน์แรก ก็จะหาได้ค่ะ

ต่อไปมาแก้ระบบสมการค่ะ
พยายามจัดรูป โดยการแยกตัวประกอบ
จาก (1) ดึง a ออก
a(1 + r + r² + r³) = 15
จัดรูป
a( 1 + r +r²(1 + r) ) = 15
a( r + 1+r²(r + 1) ) = 15
ในวงเล็บมองว่าดึง (r + 1) ออกมาอีก จะได้แบบนี้ค่ะ
a(r + 1)(r² + 1) = 15 -------(3)

จาก (2) ดึง a² ออกก่อน
แล้วเอาที่เหลือในวงเล็บไปแยกตัวประกอบ จะได้แบบนี้

a²(r²+ 1)(r⁴ +1) = 85    ---------(4)

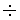
เอา (4) (3) จะได้

a2(r2+ 1)(r4 +1)

a(r + 1)(r2 + 1)

=

85

15

ตัดกันได้เหลือ

a(r4 +1)

(r + 1)

=

17

3

a =

17(r + 1)

3(r4 +1)

แทนใน(3)
จะได้

17(r + 1)

3(r4 +1)

(r + 1)(r² + 1) = 15

17(r + 1)(r + 1)(r² + 1) = 45(r⁴ + 1)
คูณกระจายให้หมด แล้วจัดรูปให้ข้างนึงเป็นศูนย์ จะได้
28r⁴ - 34r³ - 34r² - 34r + 28 = 0
ทอนเป็นอย่างต่ำ จะได้

14r⁴ - 17r³ - 17r² - 17r + 14= 0

แยกตัวประกอบโดยการ เอาไปหารสังเคราะห์
จะได้ r = 2, r =

1

2

เอา r แต่ละค่าที่ได้ไปแทน เพื่อหาค่า a ค่ะ
ถ้า r = 2 จะได้ a = 1
แทนแล้วได้ 4 พจน์แรกเป็น 1, 2, 4, 8
ผลคูณได้ = 64 ตอบค่ะ

ถ้า r =

1

2

จะได้ a = 8
แทนแล้วได้ 4 พจน์แรกเป็น 8, 4, 2, 1
ผลคูณได้ = 64 เท่าข้างบนเลย