 |
 |
|
|
Dektalent ช่วยให้การเรียนคณิตศาสตร์ กลายเป็นเรื่องง่าย
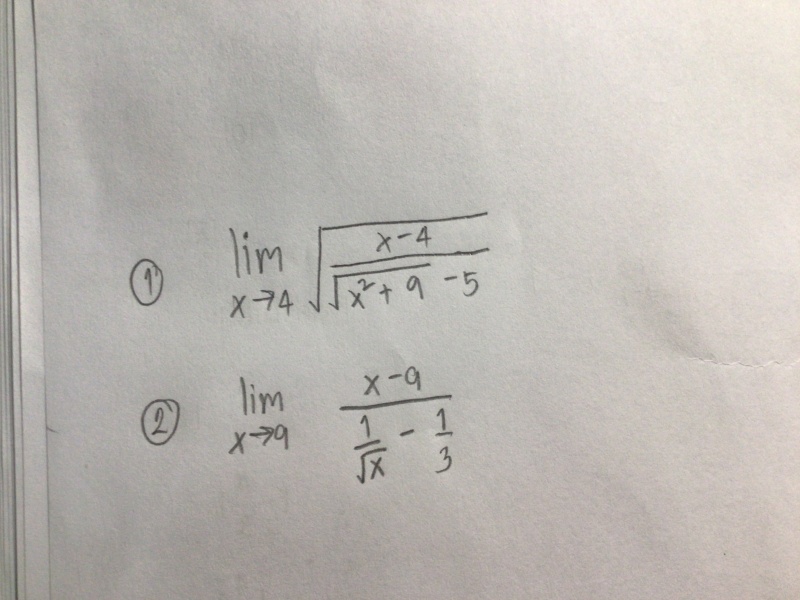
| lim |
x 4 |
|
| lim |
| x4 |
|
| lim |
| x4 |
|
| lim |
| x4 |
|
| lim |
| x4 |
|
| lim |
| x4 |
|
| lim |
| x4 |
|
|
อยากเก่งคณิต อยากทำโจทย์แบบนี้ได้ มาสมัครเรียนคอร์สคณิตออนไลน์กับครูพี่โต๋กันค่ะ เรียนด้วยคลิป VDO พร้อมแบบฝึกหัด ไม่เหนื่อย ไม่ร้อน ไม่ต้องเดินทาง เรียนได้ 24 ชม. ไม่ต้องนัดเวลา ทบทวนได้ ถามได้ครูพี่โต๋ตอบเอง สนใจสมัครได้เรียนได้ทุกวัน
| lim |
| x9 |
| x - 9 | ||||||||
|
| lim |
| x9 |
| x - 9 | ||||||||||
|
| lim |
| x9 |
(x - 9)(3
| ||||
3 -
|
| lim |
| x9 |
(
| ||||||||||||
- (
|
|
| lim |
| x9 |
(
| ||||||||
| - 1 |
อยากเก่งคณิต อยากทำโจทย์แบบนี้ได้ มาสมัครเรียนคอร์สคณิตออนไลน์กับครูพี่โต๋กันค่ะ เรียนด้วยคลิป VDO พร้อมแบบฝึกหัด ไม่เหนื่อย ไม่ร้อน ไม่ต้องเดินทาง เรียนได้ 24 ชม. ไม่ต้องนัดเวลา ทบทวนได้ ถามได้ครูพี่โต๋ตอบเอง สนใจสมัครได้เรียนได้ทุกวัน
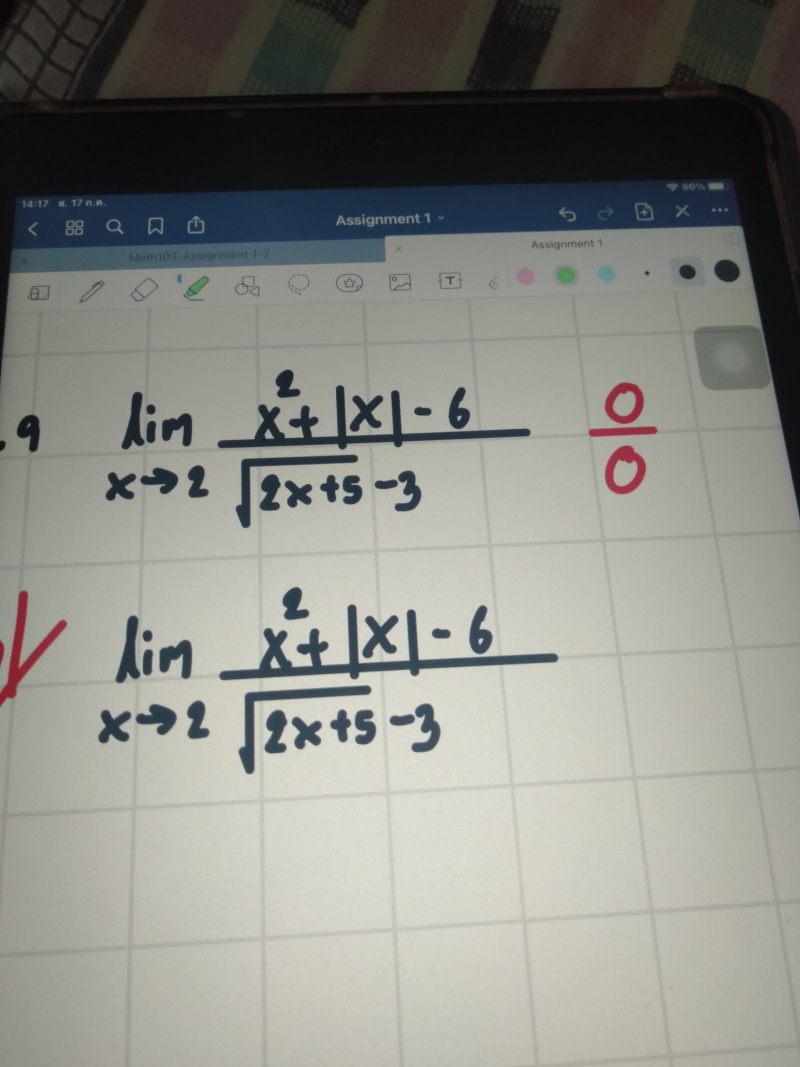
| lim |
| n2 |
| x2 + |x| - 6 | ||||
|
| ||||
|
| lim |
| n2 |
(x2 + |x| - 6)(
| ||||||||
(
|
| lim |
| n2 |
(x2 + |x| - 6)(
| ||||
| 2x + 5 - 9 |
| lim |
| n2 |
(x2 + |x| - 6)(
| ||||
| 2x - 4 |
| lim |
| n2 |
(|x| + 3)(|x| - 2) (
| ||||
| 2(x - 2) |
2 ดังนั้น
| lim |
| n2 |
(x + 3)(x - 2) (
| ||||
| 2(x - 2) |
| lim |
| n2 |
(x + 3)(
| ||||
| 2 |
(2 + 3)(
| ||||
| 2 |
| 5 6 |
| 2 |
อยากเก่งคณิต อยากทำโจทย์แบบนี้ได้ มาสมัครเรียนคอร์สคณิตออนไลน์กับครูพี่โต๋กันค่ะ เรียนด้วยคลิป VDO พร้อมแบบฝึกหัด ไม่เหนื่อย ไม่ร้อน ไม่ต้องเดินทาง เรียนได้ 24 ชม. ไม่ต้องนัดเวลา ทบทวนได้ ถามได้ครูพี่โต๋ตอบเอง สนใจสมัครได้เรียนได้ทุกวัน
| 5 |
|
| 5 |
|
| 5 |
|
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| -4 |
| 5 |
| 1 | |||
5
|
| 1 | |||
5
|
| 1 |
| 524 |
| 1 |
| 80 |
อยากเก่งคณิต อยากทำโจทย์แบบนี้ได้ มาสมัครเรียนคอร์สคณิตออนไลน์กับครูพี่โต๋กันค่ะ เรียนด้วยคลิป VDO พร้อมแบบฝึกหัด ไม่เหนื่อย ไม่ร้อน ไม่ต้องเดินทาง เรียนได้ 24 ชม. ไม่ต้องนัดเวลา ทบทวนได้ ถามได้ครูพี่โต๋ตอบเอง สนใจสมัครได้เรียนได้ทุกวัน
หรือคุณสามารถ สมัครสมาชิกได้ฟรี สมัครวันนี้รับสิทธิ์เข้าเรียนคอร์สออนไลน์ฟรี 5 ชั่วโมง!
DekTalent.com คือเว็ปไซท์เรียนพิเศษแนวใหม่ ผ่านคลิปวีดีโอบนเว็ปไซท์ สามารถเรียนได้จากทุกที่ ทุกเวลา ไม่ต้องเดินทาง เลือกบทเรียนเองได้อย่างอิสระ เข้าเรียนได้ 24Hr ด้วยหลักสูตรการเรียนการสอน ที่ได้มาตรฐานตามกระทรวงศึกษาธิการ
