ถามการบ้านครับ เรื่อง จำนวนเชิงซ้อน

ให้ z = a + bi แล้วแทนลงไปค่ะ
ตามสูตร |z| =

a2 + b2

จะสมมติให้ |z| = r ก่อนค่ะ

แทนแค่นี้ก่อน
จาก z|z| + 2z + i = 0
แทน |z| = r จะได้
zr + 2z + i = 0
จัดรูป
zr + 2z = -i
z(r + 2) = -i
      z =

-i

r + 2

เขียนให้เห็นส่วนจริง ส่วนจินตภาพชัดๆ ได้แบบนี้
      z = 0 +

-1

r + 2

i

จากที่สมมติไว้ว่า z = a + bi จะได้
a = 0
b =

-1

r + 2

** เก็บไว้ก่อน

b คือ ส่วนจินตภาพ ก็คือสิ่งที่โจทย์ถามนะ

จาก |z| =

a2 + b2

แทนค่า
r =

0 + b2

r =

b2

เป็นรากเลขคู่ ติดค่าสัมบูรณ์ไว้ด้วยนะ
r = |b|
จะได้
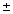
r = b

--------------
ถ้า r = b
จาก
b =

-1

r + 2

จะได้
b =

-1

b + 2

แก้สมการ หา b ได้
b(b + 2) = -1
b² + 2b = -1
b² + 2b + 1 = 0
แยกตัวประกอบได้
(b + 1)(b + 1) = 0
b = -1

เอาไปตรวจคำตอบ
จาก z = a + bi ตอนนี้จะได้
z = 0 - i
|z| =

02 + (-1)2

|z| = 1
เอาไปแทนที่โจทย์ เพื่อตรวจคำตอบ
จาก z|z| + 2z + i = 0

ทำฝั่งซ้ายดูว่าเท่ากับฝั่งขวามั้ย
(0 - i)(1) +2(0 - i) + i
= -i - 2i + i
= -2i
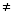
0 งั้นผิดนะ คำตอบนี้ใช้ไม่ได้

------------------
อีกกรณี
ถ้า r = -b
จาก
b =

-1

r + 2

จะได้
b =

-1

-b + 2

แก้สมการ หา b ได้
b(-b + 2) = -1
-b² + 2b = -1
0 = b² - 2b - 1
แยกไม่ลงตัวใช้สูตร
b =

-(-2) 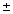   (-2)2 - 4(1)(-1)

2(1)

b =

2    8

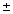2

b =

2 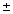2    2

2

มองว่าแยกหารย่อย แล้วตัดทอนได้ เหลือ
b = 1

2

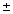
ตอนนี้ได้ 2 ค่า คือ
b = 1 +

2

, 1 -

2

เอาไปแทนค่าที่โจทย์เพื่อตรวจคำตอบ
ทำเหมือนกรณีที่แล้วเลย
ตรงนี้แทนเองนะ

ตรวจแล้วจะได้
b = 1 -

2

เป็นคำตอบที่ใช้ได้ค่ะ

:) ยินดีด้วยมากจ้า