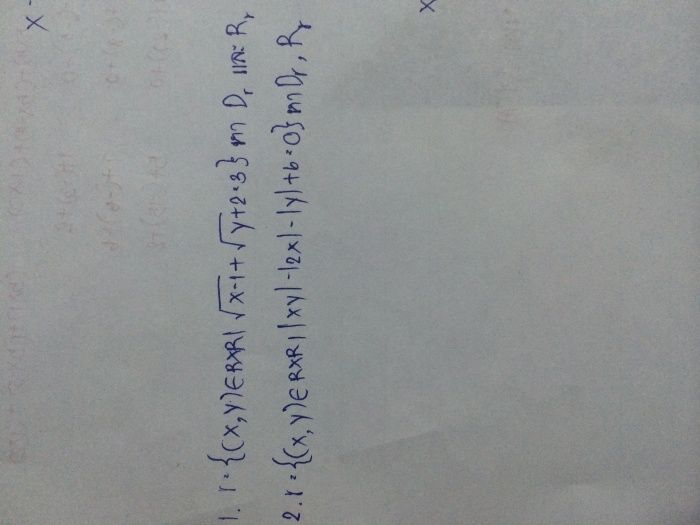ถามโจทย์เรื่องโดเมน เรนจ์ครับ

ข้อ 1

x - 1

+

y

+ 2 = 3
จากโจทย์จะได้ก่อนเลยว่า
x - 1 0 x 1
y 0
เพราะว่าอยู่ในรูทค่ะ

จะหาโดเมน ให้จัดรูปให้เป็น y ในเทอม x

x - 1

+

y

+ 2 = 3

y

= 3 - 2 -

x - 1

y

= 1 -

x - 1

เพราะว่า

y

0 เสมอ ดังนั้น 1 -

x - 1

0 ด้วย

แก้อสมการ 1 -

x - 1

0
ลองทำดู ใช้วิธียกกำลังสองก็ได้ค่ะ
แล้วเอาไปอินเตอร์เซคกับ เงื่อนไข x ที่ได้จากโจทย์ (x 1 ) จะได้โดเมนค่ะ

-----
หาเรนจ์ จัด x ในเทอม y

x - 1

= 3 - 2 -

y

x - 1

= 1 -

y

แล้วคิดสไตล์เดียวกับตอนหาโดเมนเลย
เพราะว่า

x - 1

0 เสมอ ดังนั้น 1 -

y

0 ด้วย

แก้อสมการ

y

0 ได้ค่า y แล้วเอาไปอินเตอร์เซคกับ เงื่อนไข y (y 0 )

ข้อ 2
|xy| - |2x| - |y| + 6 = 0

ตรง |xy| สามารถเขียนเป็นแบบนี้ได้ |x||y|

จะได้เป็น
|x||y| - |2x| - |y| + 6 = 0

หาโดเมน
|x||y| - |2x| - |y| + 6 = 0
|x||y| - |y| = |2x| - 6
|y|(|x| - 1) = |2x| - 6
|y| =

|2x| - 6

|x| - 1

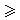
เพราะว่า |y| 0 เสมอ จะได้

|2x| - 6

|x| - 1

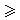
0 ด้วย

แก้อสมการนี้

|2x| - 6

|x| - 1

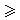
0

จะได้โดเมนค่ะ

----
การหาเรนจ์
|x||y| - |2x| - |y| + 6 = 0
จัดให้เป็น x ในเทอม y ก็คือดึง |x| ออกมา พวก y จะได้ย้ายไปฝั่งตรงข้ามให้หมด
|x||y| - |2||x| = |y| - 6
|x|(|y| - 2) = |y| - 6
|x| =

|y| - 6

|y| - 2

แล้วคิดสไตล์เดียวกับตอนหาโดเมนเลย
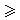
เพราะว่า |x| 0 เสมอ ดังนั้น

|y| - 6

|y| - 2

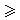
0 ด้วย

แก้อสมการ

|y| - 6

|y| - 2

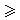
0
ก็จะได้เรนจ์ค่ะ