พี่โต๋ช่วยทำข้อ 18 22 26 หน่อยค่ะ

โจทย์บอกจุดยอดคือ (3,3)
จาก p(x) = ax² + bx + c
ใช้สูตรหาจุดยอด
x =

-b

2a

3 =

-b

2a

6a = -b
b = -6a    -------(เก็บไว้ก่อน)

y =

4ac - b2

4a

3 =

4ac - b2

4a

12a = 4ac - b²    ----------(เก็บไว้ก่อน)

ต่อไปหาจุดตัด ของพาราโบลาทั้งสอง ให้
y = ax² + bx + c    ----------(1)
y = x²    --------(2)

จับสองสมการเท่ากันได้นะ
ax² + bx + c = x[^2
จัดรูป
ax² - x² + bx + c = 0
(a - 1)x² + bx + c = 0
แก้สมการหาค่า x ได้จากสูตร
x =

-b 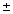   b2 - 4ac

2a

โจทย์บอกว่า มีจุดตัดเดียว ดังนั้น ตรงในรูท ต้องเท่ากับศูนย์ จะได้
b² - 4ac = 0
แทนค่า a,b,c ของสมการนี้ (a - 1)x² + bx + c = 0 ลงไปในสูตร
b² - 4(a - 1)c = 0
จัดรูป
b² - 4ac + 4c = 0
เอาที่เก็บไว้ข้างบนมาแทน
-12a + 4c = 0
4c = 12a
c = 3a เก็บไว้ก่อน

-----------------

จาก p(x) = ax² + bx + c
กราฟต้องผ่านจุดยอดแน่นอนนะ แทนค่าจุด (3,3) ได้
3 = a(3²) + b(3) + c
3 = 9a + 3b + c
จากที่เก็บไว้ b = -6a แทนค่าเลย
3 = 9a + 3(-6a) + c
จากที่หามาได้ว่า c = 3a แทนค่าเลย
3 = 9a + 3(-6a) + 3a
แก้สมการค่ะ
3 = 9a - 18a + 3a
3 = -6a
a =

-1

2

ตอบค่ะ

ตามนี้ค่ะ