ใช้เรื่องอินทิเกรต
จาก f''(x) = ax + b
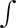
f''(x) dx = f'(x) = a
+ bx + C
1 ----- (1)
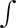
f'(x) dx = f(x) =

+ b
+ C
1x + C
2 ------(2)
รู้ว่า f(0) = 2
แทนเลยค่ะ
จาก f(x) จะได้
2 =

+ b
+ C
1(0) + C
2
2 = C2 เก็บไว้ก่อน
จากที่รู้ว่า f มีจุดต่ำสุดสัมพัทธ์ที่ (1,-5)
ตรงจุดต่ำสุดสัมพัทธ์ ความชัน จะเท่ากับศูนย์
ความชัน ก็คือ m ซึ่งก็คือ f'(x)
หรือบอกว่า เส้นโค้งนี้ ตรง x = 1 มี f'(x) = 0
ดังนั้นเอา f'(x) มาใช้ได้ แทน x = 1 จะได้ f'(x) = 0
จาก (1)
f'(x) = a
+ bx + C
1
แทนเลยนะ
0 = a
+ b(1) + C
1
0 =
+ b + C
1 -----(3)
รู้ว่า ผ่านจุด (1,-5) เอาไปแทนที่ f(x) ได้
จาก
f(x) =

+ b
+ C
1x + C
2 ------(2)
แทนค่ะ แทน C
2 ที่รู้แล้วไปด้วย
-5 =

+ b
+ C
1(1) +
2
-5 =
+
+ C
1 + 2
-5 -2 =
+
+ C
1
-7 =
+
+ C
1 --------(4)
ที่เหลือ คือจัดรูปให้เจอสิ่งที่โจทย์ถาม
เอาที่จะใช้มาเขียนใกล้ๆ กัน
0 =
+ b + C
1 -----(3)
-7 =
+
+ C
1 --------(4)
เอา (3) - (4)
0 - (-7) =
+ b + C
1 - (
+
+ C
1)
7 =
+
7 =
+
7 =
+
โจทย์ถาม
+
ตอบ 7 ค่ะ