สอบถามเรื่องโจทย์ทฤษฎีบทพีทาโกรัสค่ะ

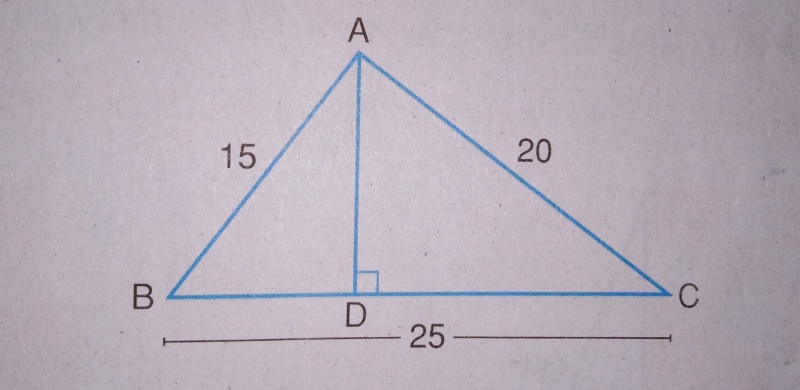
ให้ BD ยาว x หน่วย
ดังนั้น DC ยาว 25 - x หน่วย
ดูรูป ABD เป็นสามเหลี่ยมมุมฉาก
จากทฤษฎีบทพีทากอรัส จะได้
AB² = BD² + AD²
ย้ายข้างนิดหน่อย จะได้
AB² - BD² = AD² ----- (1) เก็บไว้ก่อน

ดูรูปขวาบ้าง ADC เป็นสามเหลี่ยมมุมฉาก
จะได้
AC² = DC² + AD²
ย้ายข้าง
AC² - DC² = AD² ----- (2)

ดู (1) กับ (2) จะเห็นว่า ข้างนึงเป็น AD² เหมือนกัน งั้นจับอีกฝั่งเท่ากันเลย
AB² - BD² = AC² - DC²
แทนสิ่งที่รู้ลงไป
15² - x² = 20² - (25 - x)²
แก้สมการจะได้ x ค่ะ แก้เลยนะ
ตรงวงเล็บยกกำลังสอง อย่าลืมว่า ต้องกระจายแบบกำลังสองสมบูรณ์
225 - x² = 400 - (625 - 50x + x²)
225 - x² = 400 - 625 + 50x - x²
คิดเลข คิดตัวแปร อะไรลบกันหมดไปก็ลบไปเลยค่ะ เหลือแค่นี้
225 - 400 + 625 = 50x
450 = 50x

450

50

= x
x = 9

x คือ ความยาว BD นะ แต่โจทย์ถาม AD
แทน BD = 9 ใน (1)
จาก AB² - BD² = AD²
แทนสิ่งที่รู้
15² - 9² = AD²
225 - 81 = AD²
144 = AD²
12² = AD²
12 = AD
ตอบ AD ยาว 12 หน่วยค่ะ

จริงๆ พอได้ BD = 9 แล้ว ถ้าจำอัตราส่วนในสามเหลี่ยมมุมฉากได้
ก็จะรู้ว่าข้อนี้คือ 3: 4 : 5 จะตอบ AD = 12 ได้เลยค่ะ
ถ้าจำไม่ได้ก็คิดแบบสมการข้างบนที่ทำให้ดูค่ะ