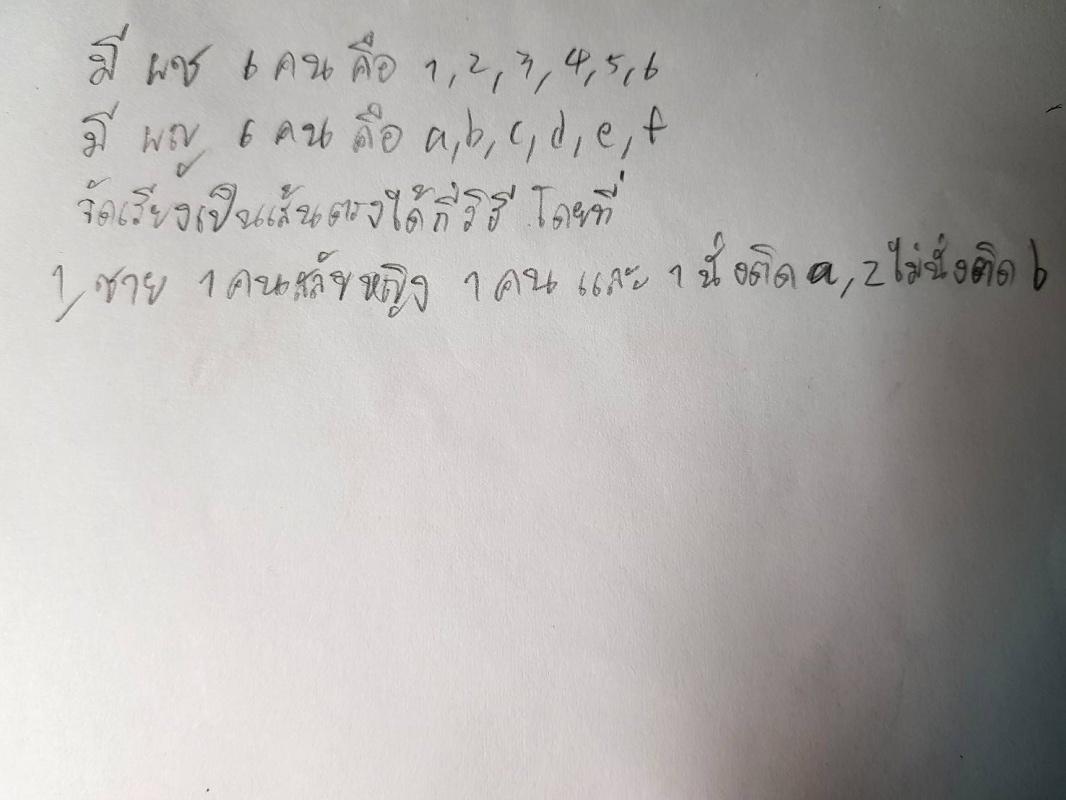ถามการบ้าน ความน่าจะเป็นครับ

จำนวนวิธีที่ 1 ติด a และ 2 ไม่ติด b = (วิธีที่ 1 ติด a) - (วิธีที่ 1 ติด a และ 2 ติด b)

ค่อยๆ หาทีละอันแล้วเอามาลบกันค่ะ

----------------------------
วิธีที่ 1ติดa >>> จับมัดเลยนะ เขียนเป็น 1a (ชญ)

ลองเขียนคนอื่นๆ ยืนสลับก่อน จะได้
ช ญ ช ญ ช ญ ช ญ ช ญ

แทรก 1a ลงไป จะแทรกได้ตามนี้
_ ช ญ _ ช ญ _ ช ญ _ ช ญ _ ช ญ _       ได้ 6 วิธี

ถ้าสลับเป็น a1 (ญช) จะแทรกได้ตามนี้

ช _ ญ ช _ญ ช _ญ ช _ญ ช _ญ       ได้ 5 วิธี

ชายคนอื่นๆ สลับได้อีก 5!
หญิงคนอื่นๆ สลับได้อีก 5!
สลับเป็น ญ ขึ้นต้นบ้าง ได้อีก ตรงนี้ 2
สรุป ชาย หญิง นั่งสลับ และ 1 ติด a = (6+5) 5! 5! 2 = 225!5!

-----------------------
วิธีที่ 1ติดa และ 2ติดb
แยก 2 คู่นี้ออกมาต่างหาก แล้วค่อยเอาไปแทรกทีหลังค่ะ

เขียนคนอื่นๆ ก่อน

ช ญ ช ญ ช ญ ช ญ (เหลือแค่ 4 คู่นะ)

แทรก 1a ได้ตามนี้
_ ช ญ _ ช ญ _ ช ญ _ ช ญ _        เฉพาะที่แทรก 1a ได้ 5 วิธี

สมมติแทรก 1a ไปซักที่นึง
1 a ช ญ ช ญ ช ญ ช ญ

ต่อไปคิดว่า แทรก 2b (ชญ) ไปตรงไหนได้บ้าง จะได้ตามนี้

_ 1 a_ ช ญ_ ช ญ _ ช ญ _ ช ญ _       ได้ 6 วิธี

สรุป ถ้าแทรก 1a กับ 2b จะได้ 56 = 30 วิธี


ทำ ทำนองเดียวกันค่ะ ตรงนี้ไปเขียนเองนะคะ

ถ้าเป็น a1 แทรกบ้าง จะแทรกได้อีก 4 วิธี
ลองเขียน a1 ลงไป จะแทรก b2 ได้อีก 5 วิธี

สรุป ถ้าแทรก a1 กับ b2 จะได้ 45 = 20 วิธี

อย่าลืม
ชายคนอื่นๆ สลับได้ 4! (เพราะเหลือ 4 คน)
หญิงคนอื่นๆ สลับได้ 4! (เพราะเหลือ 4 คน)
สลับเป็น ญ ขึ้นต้นบ้าง ได้อีก ตรงนี้ 2

สรุป วิธี 1ติดa และ 2 ติด b = (30+20)4!4! 2 = 1004!4!

----------------------------------------

เอาไปเข้าสมการตอนแรกค่ะ
จำนวนวิธีที่ 1 ติด a และ 2 ไม่ติด b = (วิธีที่ 1 ติด a) - (วิธีที่ 1 ติด a และ 2 ติด b)

แทนค่าคิดเลขก็จะได้คำตอบ